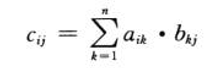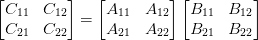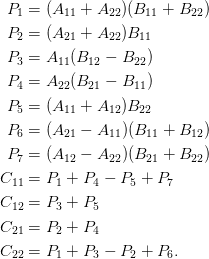function squareMatrixMultiplyStrassen(A, B) {
function getMatrix(M, x, y, n) {
var N = [];
for (var i = 0; i < n; i++) {
N[i] = [];
for (var j = 0; j < n; j++) {
N[i][j] = M[i + y][j + x];
}
}
return N;
}
function addMatrix(A, B, type) {
var n = A.length;
var N = [];
for (var i = 0; i < n; i++) {
N[i] = [];
for (var j = 0; j < n; j++) {
N[i][j] = type === 'minus' ? (A[i][j] - B[i][j]) : (A[i][j] + B[i][j]);
}
}
return N;
}
function convertMatrix(M) {
var arr = M.toString().split(',');
var array = [];
for (var k = 0; k < arr.length; k++) {
if (arr[k]) { array.push(Number(arr[k])); }
}
var n = array.length;
var m = Math.sqrt(n);
var N = [], L = [];
N[0] = array.slice(0, n / 4);
N[1] = array.slice(n / 4, n / 2);
N[2] = array.slice(n / 2, n * 3 / 4);
N[3] = array.slice(n * 3 / 4, n);
for (var i = 0; i < m; i++) {
L[i] = [];
}
for (var l = 0; l < 4; l++) {
for (var i = 0; i < m / 2; i++) {
for (var j = 0; j < m / 2; j++) {
L[i + Math.floor(l / 2) * m / 2].push(N[l][j + i * m / 2]);
}
}
}
return L;
}
var n = A.length;
var C = [];
for (var i = 0; i < n; i++) { C[i] = []; }
if (n === 1) {
C[0][0] = A[0][0] * B[0][0];
} else {
var m = parseInt(n / 2);
var A11 = getMatrix(A, 0, 0, m);
var A12 = getMatrix(A, m, 0, n - m);
var A21 = getMatrix(A, 0, m, n - m);
var A22 = getMatrix(A, m, m, m);
var B11 = getMatrix(B, 0, 0, m);
var B12 = getMatrix(B, m, 0, n - m);
var B21 = getMatrix(B, 0, m, n - m);
var B22 = getMatrix(B, m, m, m);
var P1 = squareMatrixMultiplyStrassen(addMatrix(A11, A22), addMatrix(B11, B22));
var P2 = squareMatrixMultiplyStrassen(addMatrix(A21, A22), B11);
var P3 = squareMatrixMultiplyStrassen(A11, addMatrix(B12, B22, 'minus'));
var P4 = squareMatrixMultiplyStrassen(A22, addMatrix(B21, B11, 'minus'));
var P5 = squareMatrixMultiplyStrassen(addMatrix(A11, A12), B22);
var P6 = squareMatrixMultiplyStrassen(addMatrix(A21, A11, 'minus'), addMatrix(B11, B12));
var P7 = squareMatrixMultiplyStrassen(addMatrix(A12, A22, 'minus'), addMatrix(B21, B22));
C[0][0] = convertMatrix(addMatrix(addMatrix(P1, P4), addMatrix(P5, P7, 'minus'), 'minus'));
C[0][1] = convertMatrix(addMatrix(P3, P5));
C[1][0] = convertMatrix(addMatrix(P2, P4));
C[1][1] = convertMatrix(addMatrix(addMatrix(P1, P3), addMatrix(P2, P6, 'minus'), 'minus'));
C = convertMatrix(C);
}
return C;
}